Langsung ke konten utama

Jajar genjang

A. Pengertian Jajar Genjang atau Jajaran Genjang

Jajar genjang adalah bangun datar 2 dimensi yang tersusun oleh 2 pasang sisi yang sama panjang dan sejajar serta mempunyai 2 pasang sudut yang sama besar (pasangan sudut lancip dan pasangan sudut tumpul). Dalam Bahasa inggris jajar genjang disebut parallelogram. Berikut rumus jajar genjang yang dijelaskan,
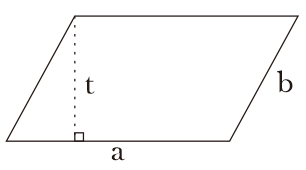
Rumus Jajar Genjang
a = sisi alas, b = sisi miring, dan t = tinggi
NamaRumus
Keliling (Kll)Kll = 2 × (a + b)
Luas (L)L = a × t
Sisi Alas (a)a = (Kll ÷ 2) – b
Sisi Sisi Miring (b)a = (Kll ÷ 2) – a
t diketahui Lt = L ÷ a
a diketahui La = L ÷ t


B. Sifat-Sifat Jajar Genjang

Rumus Jajar Genjang
  1. Mempunyai 2 pasangan sisi yang sama panjang
  2. Tinggi jajar genjang diperoleh dari garis yang melalui salah satu titik sudut ke sisi lainnya, sehingga membentuk sudut siku-siku pada sisi tersebut.
  3. Mempunyai 2 pasangan sudut yang sama besar (pasangan sudut tumpul dan pasangan sudut lancip)
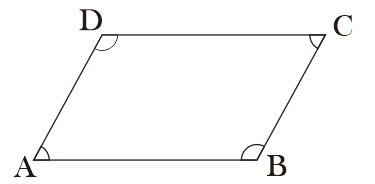
    Sudut jajar genjang
    Pada bangun jajar genjang di atas berlaku ∠BAD = ∠BCD (pasangan sudut lancip) dan ∠ABC = ∠ADC (pasangan sudut tumpul).
  4. Salah satu sudut lancip dijumlahkan dengan salah satu sudut tumpul menghasilkan nilai 180°.
  5. Sudut yang saling berhadapan mempunyai besar yang sama
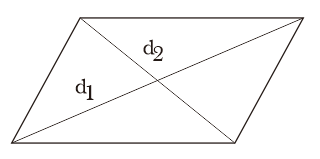
  6. Mempunyai 2 diagonal dengan panjang yang berbeda.
    Diagonal jajar genjang

C. Rumus Jajar Genjang | Luas, Tinggi, Sisi, dan Rumus Keliling Jajar Genjang

NamaRumus
Keliling (Kll)Kll = 2 × (a + b)
Luas (L)L = a × t
Sisi Alas (a)a = (Kll ÷ 2) – b
Sisi Sisi Miring (b)a = (Kll ÷ 2) – a
t diketahui Lt = L ÷ a
a diketahui La = L ÷ t

Contoh 1: Menggunakan Rumus Luas Jajar Genjang dan Rumus Keliling Jajar Genjang

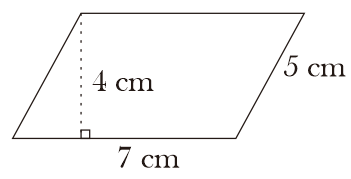
Diketahui dengan sisi alas 7 cm, sisi miring 5 cm dan tinggi 4 cm. Buatlah ilustrasi gambar jajar genjang beserta hitunglah luas dan keliling jajar genjang tersebut!
Diketahui: 
a = 7 cm, b = 5 cm, dan t = 4 cm
Ditanya:
Ilustrasi gambar, luas, dan keliling jajar genjang!
Penyelesaian:
Ilustrasi Gambar
Ilustrasi gambar jajar genjang
L = a × t
L = 7 cm × 4 cm
L = 28 cm²

Kll = 2 × (a + b)
Kll = 2 × (7 cm + 5 cm)
Kll = 2 × 12 cm
Kll = 24 cm
Jadi, Luas jajar genjang adalah 28 cm² dan keliling jajar genjang adalah 24 cm.

Komentar

Posting Komentar

Postingan populer dari blog ini

UKURAN PANCARAN DATA TUNGGAL

Hellaaaw, readers! Pembahasan diblog kali ini masih saudaraan sama materi yang sebelomnya hahhaahaha Okee cusss ya readersss... Ukuran pancaran data tunggal yang gua bahas kali ini ada 4, yaitu : 1.       Jangkauan Data Jangkauan data adalah selisih nilai tertinggi dengan nilai terendah dari suatu data. Jangkauan sering disebut juga RANGE . Jangkauan = nilai tertinggi – nilai terendah 2.       Kuartil Kuartil adalah membagi sekumpulan data menjadi empat bagian yang sama setelah data diurutkan. KUARTIL BAWAH ( Q 1 ) = ¼ ( n + 1 ) KUARTIL TENGAH atau MEDIAN (Q 2 ) = ½ ( n + 1 ) KUARTIL ATAS (Q 3 ) = ¾ (n + 1) 3.       Jangkauan Interkuartil Jangkauan interkuartil adalah selisih antara KUARTIL ATAS (Q 3 ) dengan KUARTIL BAWAH ( Q 1 ) ( J k ) = (Q 3 ) - (Q 1 ) 4.       Jangkauan Semiinterkuartil Jangkauan semiinterkuartil adalah setengah dari...
Posting Komentar
Baca selengkapnya

Balok

hai hai hai reader! kali ini gua akan membahas balok... 1. Pengertian balok Balok  adalah bangun ruang yang memiliki tiga pasang sisi yang ukurannya sama dan saling berhadapan serta memiliki bentuk persegi panjang.   Balok  adalah bangun ruang tiga dimensi yang dibentuk oleh tiga pasang persegi atau persegi panjang, dengan paling tidak satu pasang di antaranya berukuran berbeda. Balok memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Balok yang dibentuk oleh enam persegi sama dan sebangun disebut sebagai kubus. Jadi, sebagaimana halnya kubus yang memiliki 6 (enam) sisi, pada balok pun demikian, namun perbedaanya kalau pada kubus keenam sisinya mempunyai bentuk dan ukuran yang sama yaitu berbentuk persegi. Kalau pada balok memiliki tiga pasang sisi yang ukurannya sama besarnya dan berbentuk persegi panjang. Untuk lebih jelansnya memahami pengertian balok ini, silahkan perhatikan gambar balok di bawah ini! Gambar: Balok ABCD.EFGH Pada gambar balok ABCD.EFGH...
Posting Komentar
Baca selengkapnya